RECTA DE REGRESIÓN POR EL MÉTODO DE LOS MÍNIMOS CUADRADOS
Método de cuadrados mínimos – Regresión lineal

Hemos enfatizado sobre la importancia de las representaciones gráficas y hemos visto la utilidad de las versiones linealizadas de los gráficos (
X, Y
) junto a las distintas maneras de llevar a cabo la linealización. A menudo nos confrontamos con situaciones en las que existe o suponemos que existe una relación lineal entre las variables
X
e
Y
.Surge de modo natural la pregunta: ¿cuál es la relación analítica que mejor se ajusta a nuestros datos? El
método de cuadrados mínimos
es un procedimiento general que nos permite responder esta pregunta. Cuando la relación entre las variables X e Y
es lineal,el método de ajuste por cuadrados mínimos se denomina también
método de regresión lineal
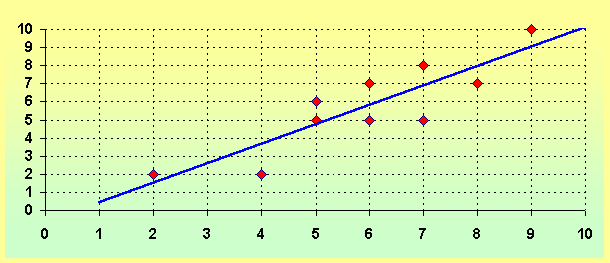
. En este capítulo discutiremos este último caso. El lector puede consultar en el Apéndice F de la Ref. [1] una discusión del caso general de cuadrados mínimos cuando el modelo es no lineal y los datos están afectados de errores.La Fig. 1 ilustra el caso lineal. La dispersión de los valores está asociada a la fluctuación de los valores de cada variable. Observamos o suponemos una tendencia lineal entre las variables y nos preguntamos sobre cuál es la
mejor recta:
y( x) =a x+b
Métodos cuantitativos de análisis gráfico
Método de cuadrados mínimos – Regresión lineal
Hemos enfatizado sobre la importancia de las representaciones gráficas y hemos visto la utilidad de las versiones linealizadas de los gráficos (
X, Y
) junto a las distintas maneras de llevar a cabo la linealización. A menudo nos confrontamos con situaciones en las que existe o suponemos que existe una relación lineal entre las variables
X eY
.Surge de modo natural la pregunta: ¿cuál es la relación analítica que mejor se ajusta a nuestros datos? El
método de cuadrados mínimos
es un procedimiento general que nos permite responder esta pregunta. Cuando la relación entre las variables
X e Y
es lineal,el método de ajuste por cuadrados mínimos se denomina también
método de regresión lineal
. En este capítulo discutiremos este último caso. El lector puede consultar en el Apéndice F de la Ref. [1] una discusión del caso general de cuadrados mínimos cuando el modelo es no lineal y los datos están afectados de errores.La Fig. 1 ilustra el caso lineal. La dispersión de los valores está asociada a la fluctuación de los valores de cada variable. Observamos o suponemos una tendencia lineal entre las variables y nos preguntamos sobre cuál es la
mejor recta:
y( x) =a x+b
(1)que representa este caso de interés.Es útil definir la función
χ2(Chi-cuadrado)[1-3]:
∑ +⋅−=ibi xai y2)(2 χ(2)que es una medida de la desviación total de los valores observados
Y i respecto de los predichos por el modelo lineal
a x+b.
Los mejores valores de la pendiente
A y la ordenada al origen b son aquellos que minimizan esta desviación total, o sea, son los valores que remplazados en la Ec.(1) minimizan la función χ 2, Ec.(2). Los parámetros a y b pueden obtenerse usando técnicas matemáticas que hacen uso del cálculo.
COEFICIENTE DE CORRELACION r DE PEARSON
Antes de introducirnos en el modelo de regresión lineal, que hace referencia a la
naturaleza de la relación entre distintas variables, pasaremos a exponer el estadístico
utilizado para medir la magnitud de la relación (supuestamente lineal) entre dichas
variables. Tiene sentido darle un tratamiento aparte por su importancia y las
continuas referencias que ofreceremos a lo largo de este texto. Comenzaremos su
desarrollo, por razones de simplicidad, para el caso particular de dos variables.
El índice numérico más común usado para medir una correlación es el “coeficiente de Pearson”. El coeficiente de Pearson (también llamado coeficiente de correlación del producto-momento), se representa con el símbolo ‘r’ y proporciona una medida numérica de la correlación entre dos variables.
Es útil reconocer la fórmula usada para calcular el coeficiente de Pearson (es posible que vea documentos en que se haga referencia a ella). Le entregamos la fórmula en una nota al pie de esta página. No deje que la fórmula lo intimide. No necesita comprender la fórmula para comprender el concepto de correlación. Aunque si hace un esfuerzo va a comprender la fórmula en poco tiempo y con claridad.
Valor del
Coeficiente de Pearson |
Grado de Correlación
entre las Variables |
r = 0
|
Ninguna correlación
|
r = 1
|
Correlación positiva perfecta
|
0 < r < 1
|
Correlación positiva
|
r = -1
|
Correlación negativa perfecta
|
-1 < r < 0
|
Correlación negativa
|
Nótese que una correlación negativa no es menos fuerte que una correlación positiva. Así, por ejemplo, un de 0,5 es tan ‘grande’ o fuerte como un de –0,5. Los signos positivos y negativos sólo indican si el valor de una variable aumenta o disminuye, respectivamente, con el aumento en el valor de la otra variable. Como usted sabe, cuando los aumentos (disminuciones) de una variable producen aumentos (disminuciones) en la otra, la relación es positiva. Es negativa cuando los aumentos (disminuciones) de una variable producen disminuciones (aumentos) en la otra.
Para datos no agrupados se calcula aplicando la siguiente ecuación:
ejemplo ilustrativo:
Con los datos sobre las temperaturas en dos días diferentes en una ciudad, determinar el tipo de correlación que existe entre ellas mediante el coeficiente de PEARSON.
X
|
18
|
17
|
15
|
16
|
14
|
12
|
9
|
15
|
16
|
14
|
16
|
18
|
SX =180
|
Y
|
13
|
15
|
14
|
13
|
9
|
10
|
8
|
13
|
12
|
13
|
10
|
8
|
SY= 138
|
Solución:
Se calcula la media aritmética:
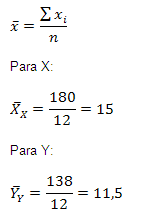
Se llena la siguiente tabla:
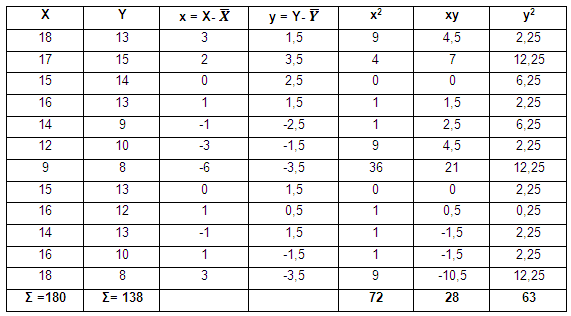
Se aplica la fórmula:
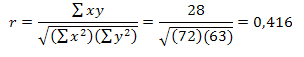
Para datos agrupados, el coeficiente de Correlación de Pearson se calcula aplicando la siguiente fórmula:
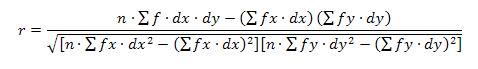
Donde
n = número de datos.
f = frecuencia de celda.
fx = frecuencia de la variable X.
fy = frecuencia de la variable Y.
dx = valores codificados o cambiados para los intervalos de la variable X, procurando que al intervalo central le corresponda dx = 0, para que se hagan más fáciles los cálculos.
dy = valores codificados o cambiados para los intervalos de la variable X, procurando que al intervalo central le corresponda dy = 0, para que se hagan más fáciles los cálculos.
Ejemplo ilustrativo:
Con los siguientes datos sobre los Coeficientes Intelectuales (X) y de las calificaciones en una prueba de conocimiento (Y) de 50 estudiantes:
N° de estudiante
|
X
|
Y
|
N° de estudiante
|
X
|
Y
|
1
|
76
|
28
|
26
|
88
|
40
|
2
|
77
|
24
|
27
|
88
|
31
|
3
|
78
|
18
|
28
|
88
|
35
|
4
|
79
|
41
|
29
|
88
|
26
|
5
|
79
|
43
|
30
|
89
|
30
|
6
|
80
|
45
|
31
|
89
|
24
|
7
|
80
|
34
|
32
|
90
|
18
|
8
|
81
|
18
|
33
|
90
|
11
|
9
|
82
|
40
|
34
|
90
|
15
|
10
|
82
|
35
|
35
|
91
|
38
|
11
|
83
|
30
|
36
|
92
|
34
|
12
|
83
|
21
|
37
|
92
|
31
|
13
|
83
|
22
|
38
|
93
|
33
|
14
|
83
|
23
|
39
|
93
|
35
|
15
|
84
|
25
|
40
|
93
|
24
|
16
|
84
|
11
|
41
|
94
|
40
|
17
|
84
|
15
|
42
|
96
|
35
|
18
|
85
|
31
|
43
|
97
|
36
|
19
|
85
|
35
|
44
|
98
|
40
|
20
|
86
|
26
|
45
|
99
|
33
|
21
|
86
|
30
|
46
|
100
|
51
|
22
|
86
|
24
|
47
|
101
|
54
|
23
|
86
|
16
|
48
|
101
|
55
|
24
|
87
|
20
|
49
|
102
|
41
|
25
|
88
|
36
|
50
|
102
|
45
|
1) Elaborar una tabla de dos variables
2) Calcular el coeficiente de correlación
Solución:
1) En la tabla de frecuencias de dos variables, cada recuadro de esta tabla se llama una celda y corresponde a un par de intervalos, y el número indicado en cada celda se llama frecuencia de celda. Todos los totales indicados en la última fila y en la última columna se llaman totales marginales o frecuencias marginales, y corresponden, respectivamente, a las frecuencias de intervalo de las distribuciones de frecuencia separadas de la variable X y Y.
Para elaborar la tabla se recomienda:
- Agrupar las variables X y Y en un igual número de intervalos.
- Los intervalos de la variable X se ubican en la parte superior de manera horizontal (fila) y en orden ascendente.
- Los intervalos de la variable Y se ubican en la parte izquierda de manera vertical (columna) y en orden descendente.
Para elaborar los intervalos se procede a realizar los cálculos respectivos:
En la variable X:

En la variable Y:
